Explicit Logic Trees ⇒ Core of Explainable AI (XAI)

First-Order & Propositional Interactive Symbolic Reasoning Engines,
built 2002–2004 as a graduate thesis🎓, now open-sourced.

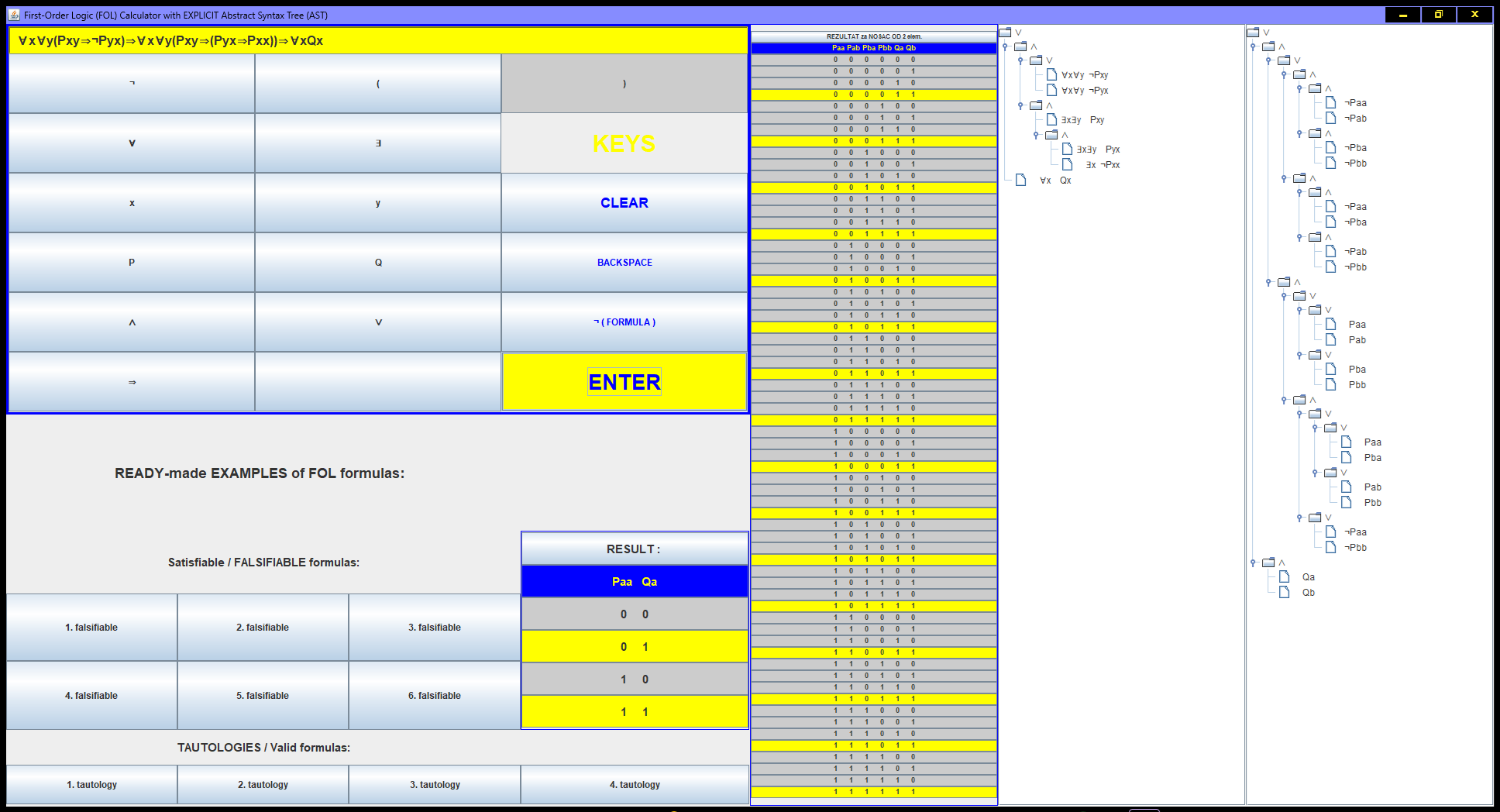
Tree Of Knowledge — preview

Originally designed for teaching and learning mathematical logic, with an explicit focus on structural reasoning and explainability.

⚠ It will work only if you have installed Java: Download recommended version

💻 Download on PC & RUN

If you’re cautious scan downloaded JAR files on: VirusTotal

Instructions

  1. Select any of the READY-MADE EXAMPLE formulas of First-Order Logic and press ENTER.

  2. Try to FOLLOW THE PATTERN you observe in the example formulas.

    Note: Predicate P may take two variables, while Q takes only one.

    Valid examples: ∀x∃y Pxy, ∀y Qy, ∃x Qx

    Invalid example: ∃x∀y Qxy

    If you make a mistake, the INVALID part of the input will be automatically removed.

    Note on syntax: Logical grouping parentheses are intentionally omitted for practical simplicity. Predicates are written in compact form: Pxy instead of P(x,y).
  3. Try the “¬ (FORMULA)” button — it negates the entire formula. Then press ENTER again and observe the changes in the calculator window.

Technical & Working Explanation

Formulas are recursively decomposed into primitive connectives {¬ (NOT), ∧ (AND), ∨ (OR)} and transformed via De Morgan laws into a Negation Normal Form (NNF) Abstract Syntax Tree (AST), with negations pushed to the atomic level.

[ChatGPT observation: “This looks like the DNA of common sense.”]

👉 Full technical description: README on GitHub

IF THIS SEEMS TOO COMPLICATED AT FIRST, PLEASE PROCEED TO THE MUCH SIMPLER PROPOSITIONAL TREE BELOW (Beginner mode).

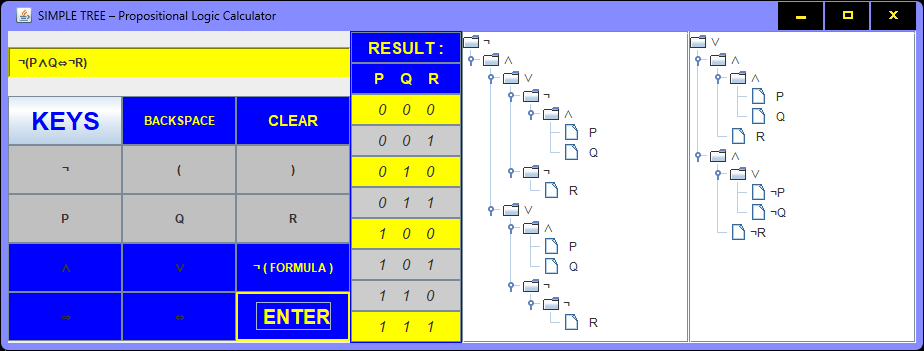
SIMPLE Tree Of Knowledge — preview

🟦 SIMPLE TREE

THE BLUE COLOR WILL GUIDE YOU STEP BY STEP.

💻 Download for PC & RUN
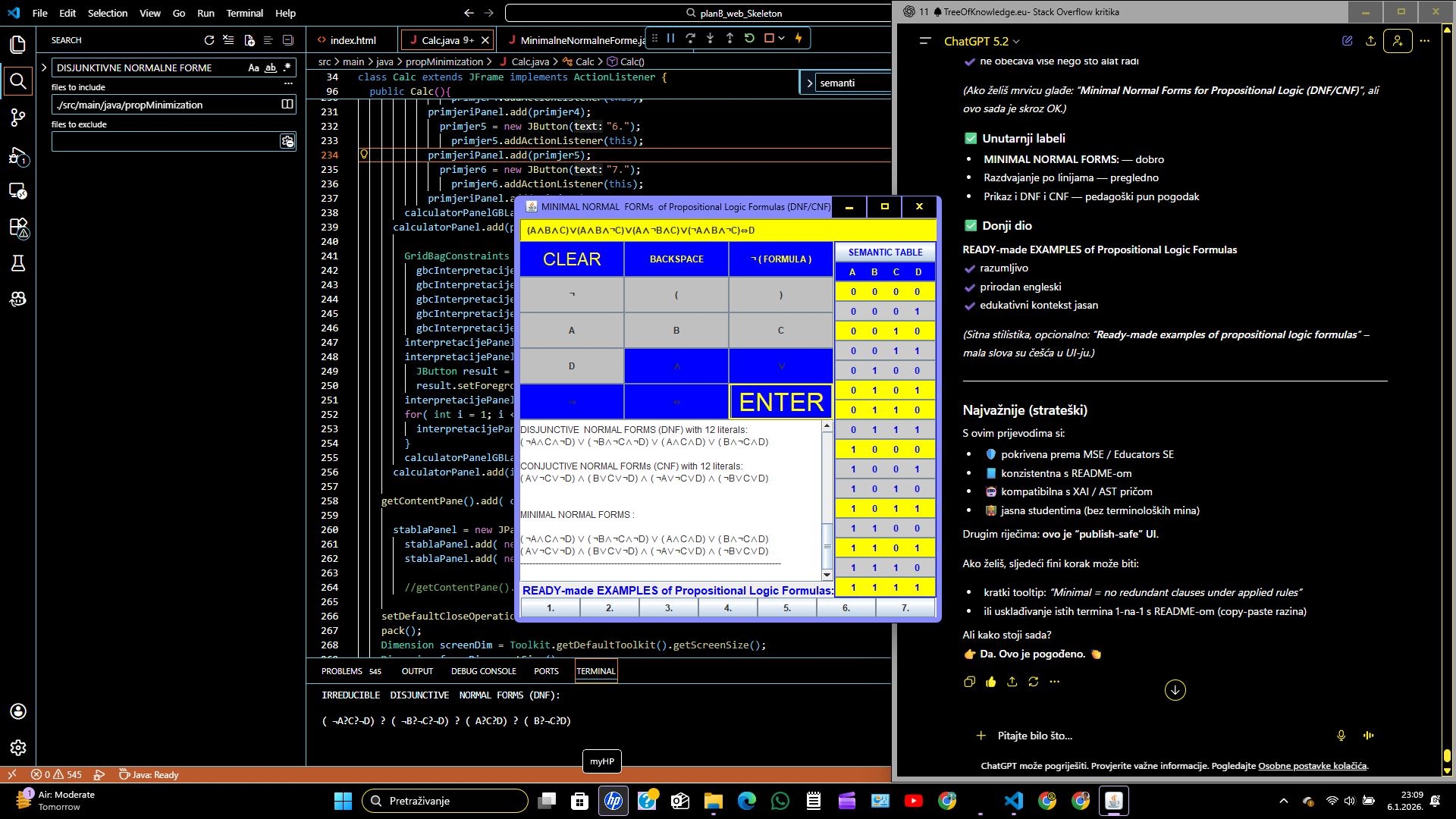
Minimization calculator for propositional logic — preview

PROPOSITIONAL logic ⇒ MINIMAL NORMAL FORMS

💻 Download 4 PC & RUN

🔄 Calculators last updated: 9. 2. 2026.

For long-term or research use, academic collaboration, or licensing inquiries — please contact the author . in

View source on GitHub

Prefer full source bundle?

⬇ Download SOURCE (ZIP)

Dedicated to every child who dies from starvation — 1 every 10 seconds, around 10,000 each day.

❤️ So if you like this project, please consider supporting a meal for a child: Mary’s Meals